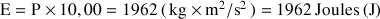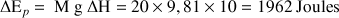Définition de base
Définition :
Le joule (du nom d'un physicien Britannique du XIX James Prescott Joule) - symbole : « J », est l'unité dérivée du système international (SI) pour quantifier l'énergie.
Remarque :
Le Système International SI, crée en 1960 mais héritier de travaux initiés dès le XVII siècle, harmonise au niveau mondial l'ensemble des unités utilisées pour quantifier des grandeurs physiques ; celles-ci sont actuellement au nombre de sept unités fondamentales :
Grandeur | Symbole de la grandeur | Unité SI | Symbole associé à l'unité |
|---|---|---|---|
Masse | M | Kilogramme | kg |
Temps | T | Seconde | s |
Longueur | L | Mètre | m |
Température | θ | Kelvin | K |
Intensité électrique | I | Ampère | A |
Quantité de matière | N | Mole | mol |
Intensité lumineuse | J | Candela | cd |
Le Système international d'unités a été adopté officiellement par tous les pays à l'exception des Etats-Unis, du Libéria et du Myanmar ; en France, la Loi peut sanctionner l'utilisation d'unités autres que celles du SI .
Définition :
D'un point de vue mécanique, l'énergie fournie par une force correspond au travail de cette force s'exprimant globalement comme étant son intensité multipliée par son déplacement.
Prenons un exemple simple, pousser une voiture en panne. La force considérée est celle fournie par le pousseur.
Tant qu'il n'y a pas de déplacement, il n'y a pas d'énergie fournie et pas de travail.
Pour accélérer (provoquer un déplacement), l'énergie fournie est d'autant plus importante que le véhicule à déplacer est lourd et donc la force nécessaire (intensité) importante.
Pour maintenir une vitesse , l'énergie fournie est d'autant plus importante que la distance à parcourir (déplacement), les frottements et résistances au déplacements importants.
Cette définition est à l'origine des expressions de l'énergie cinétique et de l'énergie potentielle.
Plus on veut déplacer rapidement le véhicule et lui donner donc de la vitesse, plus l'énergie à fournir et donc l'intensité de la force doivent être grandes :
Si le déplacement se fait selon une pente ascendante, l'énergie à fournir et donc l'intensité de la force doivent être plus importante ; l'inverse si la pente est descendante. Dans le premier cas, on augmente l'énergie potentielle fournie au véhicule, dans le second, il y a libération d'énergie potentielle diminuant le travail à fournir...
Enfin, quelque soit le cas de figure, on retrouve l'idée du premier principe : l'énergie fournie (entrée) par le travail de la force est communiquée au véhicule sous forme d'énergie cinétique et d'énergie potentielle. On observe alors (sortie) un travail communiqué au véhicule (il se déplace) et des dissipations liées notamment aux frottements (pneus/surface de roulement par exemple).
Définition :
Un joule est l'énergie nécessaire pour déplacer le point d'application d'une force valant 1,00 Newton sur une distance de 1,00 mètre et selon la direction de cette force.
Il s'agit là de la définition du travail d'une force qui est à l'origine de la définition de l'énergie du point de vue mécanique :
Remarque :
Remarque :
Homogénéité des unités
Énergie cinétique :
unité :
soit des Joules J.
Énergie potentielle :
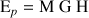unité :
soit des
donc des Joules J.
Exemple :
Quelle énergie faut-il fournir pour élever verticalement de 10,00 mètres un sac de masse M = 20 kilos ? Réponse :
P = 196,2 Newton L'énergie nécessaire pour l'élever de 10,00 mètre vaut :
Par définition, l'énergie potentielle de ce sac de 20 kg a augmentée de la même valeur, puisque
L'énergie nécessaire a été transmise et s'est conservée. |  |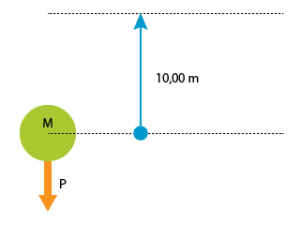
Exemple :
A quelle masse que l'on élève verticalement de 1,00 mètre correspond une énergie de 1,00 Joule dépensée ? On considérera la pesanteur valant 9,81 m / s2.
Réponse : Il s'agit du déplacement d'une force (poids) valant 1,00 Newton par définition, donc d'une masse
M = 1,00 / 9,81 soit une masse de 0,102 kilos environ.
Exemple :
Quelle est l'énergie cinétique associé à 1 m3 d'air en déplacement (vent) aux vitesses suivantes :
14 km/h correspondant dans la plupart des cas à la vitesse minimale de fonctionnement
28 km/h
90 km/h correspondant à la vitesse maximale avant arrêt de l'éolienne
On considérera une masse volumique de l'air égale à 1,2 kg/m3 (valeur à 20°C dans des conditions normales de pression).
Réponse :
km/h | m/s | M (kg) = | Ec = | |
14 | 3.9 | 1.2 | 9.07 | J |
28 | 7.8 | 1.2 | 36.30 | J |
90 | 25 | 1.2 | 375 | J |
On remarque évidemment que l'énergie cinétique n'est pas proportionnelle à la vitesse mais au carré de la vitesse : quand celle-ci double, l'énergie ne double pas mais quadruple.
Exemple :
Quelle est l'énergie potentielle libérée par 1 m3 d'eau chutant de 1,00 mètre ? de 100 mètres ?
Réponse :
M (kg) | g | H (m) | Ep = | |
1000 | 9.81 | 1 | 9810 | J |
1000 | 9.81 | 100 | 981000 | J |
L'énergie potentielle est elle proportionnelle à la masse et aux hauteurs considérées ; on remarquera les ordres de grandeur très différents entre ces deux sources d'énergie renouvelables ; il faut néanmoins relativiser de par leurs temporalités : l'eau ne chute qu'une fois alors que le vent souffle sur des durées de temps...
